
On June 23, 1993, the mathematician Andrew Wiles gave the last of three lectures detailing his solution to Fermat’s last theorem, a problem that had remained unsolved for three and a half centuries. Wiles’ announcement caused a sensation, both within the mathematical community and in the media.
Beyond providing a satisfying resolution to a long-standing problem, Wiles’ work marks an important moment in the establishment of a bridge between two important, but seemingly very different, areas of mathematics.
History demonstrates that many of the greatest breakthroughs in math involve making connections between seemingly disparate branches of the subject. These bridges allow mathematicians, like the two of us, to transport problems from one branch to another and gain access to new tools, techniques and insights.
What is Fermat’s last theorem?
Fermat’s last theorem is similar to the Pythagorean theorem, which states that the sides of any right triangle give a solution to the equation x2 + y2 = z2 .
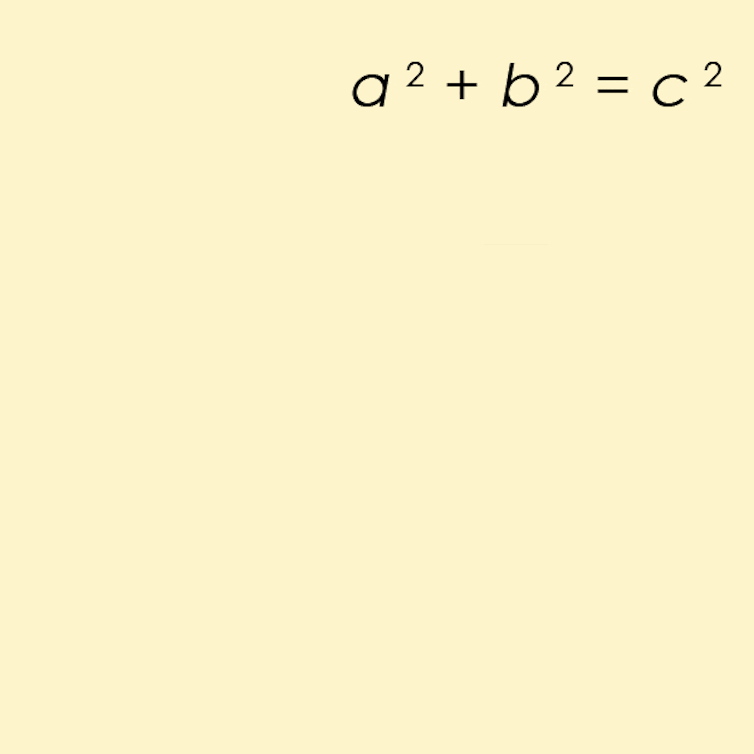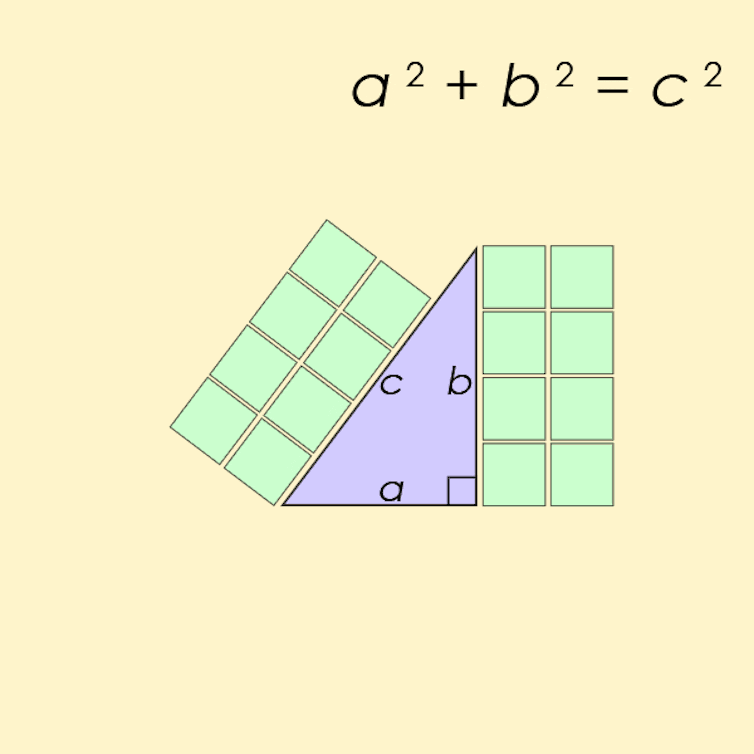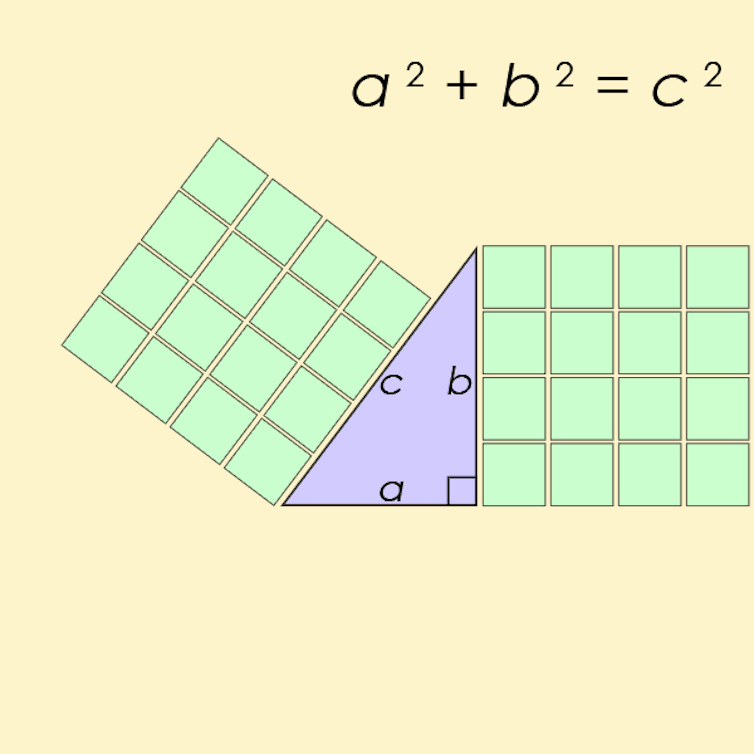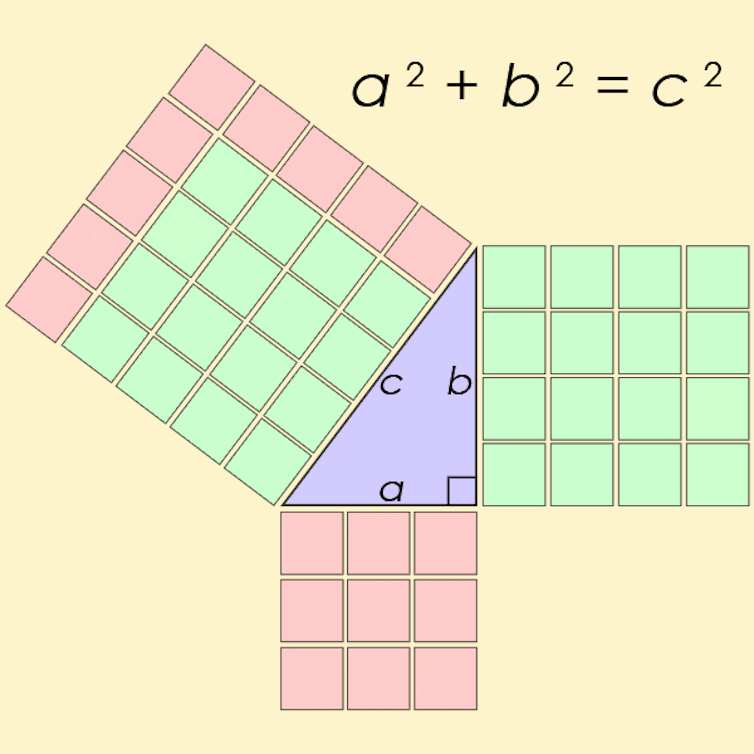
Every differently sized triangle gives a different solution, and in fact there are infinitely many solutions where all three of x, y and z are whole numbers – the smallest example is x=3, y=4 and z=5.
Fermat’s last theorem is about what happens if the exponent changes to something greater than 2. Are there whole-number solutions to x3 + y3 = z3 ? What if the exponent is 10, or 50, or 30 million? Or, most generally, what about any positive number bigger than 2?

Around the year 1637, Pierre de Fermat claimed that the answer was no, there are no three positive whole numbers that are a solution to xn + yn = zn for any n bigger than 2. The French mathematician scribbled this claim into the margins of his copy of a math textbook from ancient Greece, declaring that he had a marvelous proof that the margin was “too narrow to contain.”
Fermat’s purported proof was never found, and his “last theorem” from the margins, published posthumously by his son, went on to plague mathematicians for centuries.
Searching for a solution
For the next 356 years, no one could find Fermat’s missing proof, but no one could prove him wrong either – not even Homer Simpson. The theorem quickly gained a reputation for being incredibly difficult or even impossible to prove, with thousands of incorrect proofs put forward. The theorem even earned a spot in the Guinness World Records as the “most difficult math problem.”
That is not to say that there was no progress. Fermat himself had proved it for n=3 and n=4. Many other mathematicians, including the trailblazer Sophie Germain, contributed proofs for individual values of n, inspired by Fermat’s methods.
But knowing Fermat’s last theorem is true for certain numbers isn’t enough for mathematicians – we need to know it’s true for infinitely many of them. Mathematicians wanted a proof that would work for all numbers bigger than 2 at once, but for centuries it seemed as though no such proof could be found.
However, toward the end of the 20th century, a growing body of work suggested Fermat’s last theorem should be true. At the heart of this work was something called the modularity conjecture, also known as the Taniyama-Shimura conjecture.
A bridge between two worlds
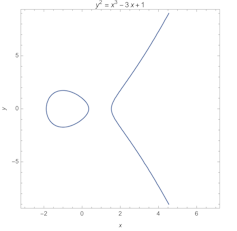
The modularity conjecture proposed a connection between two seemingly unrelated mathematical objects: elliptic curves and modular forms.
Elliptic curves are neither ellipses nor curves. They are doughnut-shaped spaces of solutions to cubic equations, like y2 = x3 – 3x + 1.
A modular form is a kind of function which takes in certain complex numbers – numbers with two parts: a real part and an imaginary part – and outputs another complex number. What makes these functions special is that they are highly symmetrical, meaning there are lots of conditions on what they can look like.

There is no reason to expect that those two concepts are related, but that is what the modularity conjecture implied.
Finally, a proof
The modularity conjecture doesn’t appear to say anything about equations like xn + yn = zn . But work by mathematicians in the 1980s showed a link between these new ideas and Fermat’s old theorem.
First, in 1985, Gerhard Frey realized that if Fermat was wrong and there could be a solution to xn + yn = zn for some n bigger than 2, that solution would produce a peculiar elliptic curve. Then Kenneth Ribet showed in 1986 that such a curve could not exist in a universe where the modularity conjecture was also true.
Their work implied that if mathematicians could prove the modularity conjecture, then Fermat’s last theorem had to be true. For many mathematicians, including Andrew Wiles, working on the modularity conjecture became a path to proving Fermat’s last theorem.
Wiles worked for seven years, mostly in secret, trying to prove this difficult conjecture. By 1993, he was close to having a proof of a special case of the modularity conjecture – which was all he needed to prove Fermat’s last theorem.
He presented his work in a series of lectures at the Isaac Newton Institute in June 1993. Though subsequent peer review found a gap in Wiles’ proof, Wiles and his former student Richard Taylor worked for another year to fill in that gap and cement Fermat’s last theorem as a mathematical truth.
Lasting consequences
The impacts of Fermat’s last theorem and its solution continue to reverberate through the world of mathematics. In 2001, a group of researchers, including Taylor, gave a full proof of the modularity conjecture in a series of papers that were inspired by Wiles’ work. This completed bridge between elliptic curves and modular forms has been – and will continue to be – foundational to understanding mathematics, even beyond Fermat’s last theorem.
Wiles’ work is cited as beginning “a new era in number theory” and is central to important pieces of modern math, including a widely used encryption technique and a huge research effort known as the Langlands Program that aims to build a bridge between two fundamental areas of mathematics: algebraic number theory and harmonic analysis.
Although Wiles worked mostly in isolation, he ultimately needed help from his peers to identify and fill in the gap in his original proof. Increasingly, mathematics today is a collaborative endeavor, as witnessed by what it took to finish proving the modularity conjecture. The problems are large and complex and often require a variety of expertise.
So, finally, did Fermat really have a proof of his last theorem, as he claimed? Knowing what mathematicians know now, many of us today don’t believe he did. Although Fermat was brilliant, he was sometimes wrong. Mathematicians can accept that he believed he had a proof, but it’s unlikely that his proof would stand up to modern scrutiny.
Maxine Calle, Ph.D. Candidate in Mathematics, University of Pennsylvania and David Bressoud, Professor Emeritus of Mathematics, Macalester College
This article is republished from The Conversation under a Creative Commons license.
Check out www.myprintshop.vip
